ABSTRACT: Remarkably few things escaped Aristotle's attention, or Darwin's for that matter. Aristotle noted regular patterns of bilateral asymmetries in animals: "In the Caribi [hermit crabs] and in the Carcini [true crabs] the right claw is invariably larger and stronger. In the Astaci [crayfish and lobsters] alone it is a matter of chance which claw is the larger, and this in either sex." (Herrick 1909). Darwin too had a hunch about asymmetries while wrestling with mechanisms of inheritance. He felt deviations from the "law of symmetry" (i.e., anomalous asymmetries in normally symmetrical organisms) would not be inherited, but the meagre evidence at his disposal dealing mainly with gross deformities, seemed to suggest otherwise (Palmer and Strobeck 1986). And so the history of the literature on morphological asymmetry progressed, fitfully and capriciously, from anecdotal observations and entertaining stories, to extensive compilations of conspicuous asymmetries (Ludwig 1932, Neville 1976). Morphological asymmetries were but one of nature's many curiosities. Rather recently, however, biologists have begun to realize that deviations from symmetry might be more than just a curiosity. One kind of asymmetry, fluctuating asymmetry, has been advanced as a tool for inferring the health or quality or developmental stability of organisms. The allure of this new and seemingly simple tool has attracted considerable recent attention (Markow 1995), but its uncritical application has also engendered much skepticism. Just how powerful is this tool, and how reliable? Perhaps very, but those wishing to apply it must recognize that the biological signal is exceedingly small, and that not all deviations from symmetry provide a useful signal. Without adequate attention to fundamental methodological and conceptual issues, statistical patterns of asymmetry variation, no matter how appealing, may be biologically meaningless. However, when used with care, fluctuating asymmetry offers a unique tool for quantitative comparisons of developmental precision among a wide range of organisms and traits.

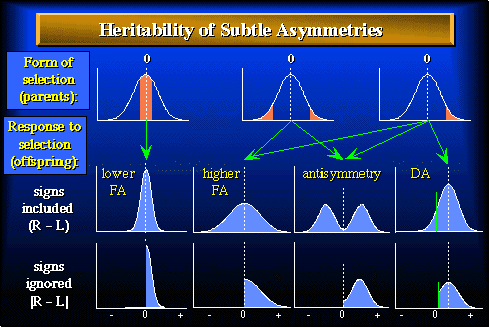
Figure 1. Frequency distributions of the difference between sides (R - L) illustrating forms of selection, and responses to selection, for subtle deviations from bilateral symmetry. Shaded areas in figures a - c indicate phenotypes selected from a parental population exhibiting fluctuating asymmetry (FA). Arrows indicate possible responses among the offspring for a particular type of selection, which are shown either as the signed value (d - g) or the absolute value (h - k) of differences between sides. Vertical dashed lines indicate the mean for each distribution. If selection for decreased (a) or increased asymmetry (b, c) yielded only lower (d, h) or higher (e, i) fluctuating asymmetry respectively in the offspring, this would suggest a heritable basis to the factors influencing developmental precision. If selection for increased asymmetry (b, c) yielded antisymmetry (f,j) or directional asymmetry (g,k) in the offspring, then deviation from symmetry may not be a reliable measure of developmental precision. A regression of the absolute value of the R-L differences of the offspring (h,i) against that of the parents (that portion of the curve to the right of the dashed line in a - c) provides a convenient measure of the heritability of developmental precision only where fluctuating asymmetry (d,e) is the only form of asymmetry present. Where either antisymmetry or directional asymmetry are present in the offspring (f,g), however, a regression of the absolute value of the R-L differences of the offspring (j,k) against that of the parents confounds the heritability of factors influencing developmental precision with those influencing asymmetry directly.
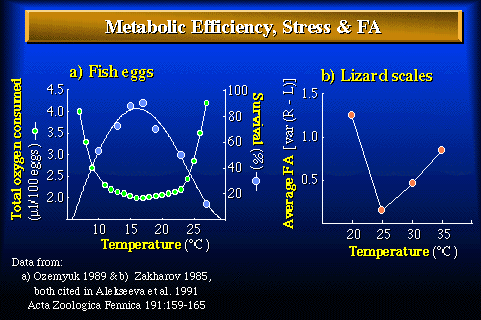
Figure 2. Relationships between metabolic efficiency (total oxygen consumed over a defined period of development), survival, fluctuating asymmetry, and temperature under laboratory conditions. a) Total oxygen consumed during one entire cleavage division (a higher value means a lower metabolic efficiency) and percent survival as a function of temperature in loach eggs (Misgurnus fossilis) (Ozernyuk 1989). b) Average fluctuating asymmetry (based on 13 scale counts) as a function of temperature in the sand lizard (Lacerta agilis) (Zakharov 1985). Both from Alekseeva et al. (1992). Although the organisms and temperature ranges are different, departures from optimum conditions during development result in lower metabolic efficiency (a) or lower developmental precision (b).
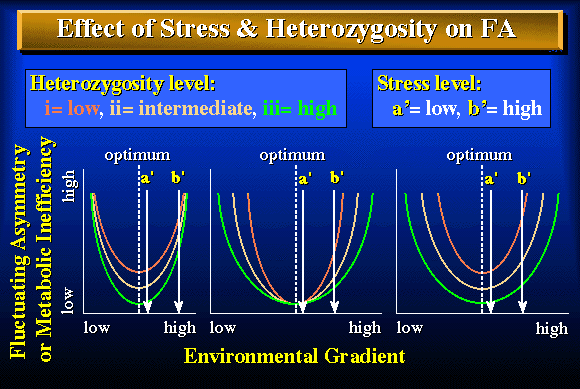
Figure 3. Three ways in which differences in heterozygosity might influence the effect of stress (deviation from the optimum) on fluctuating asymmetry (FA) or metabolic inefficiency: (a) the location of the curve at the optimum varies, (b) the shape of the curve varies but not its location at the optimum, and (c) both the shape of the curve and its location at the optimum vary. Each graph illustrates curves for three heterozygosity levels: (i) low, (ii) intermediate and (iii) high. Arrows indicate levels of high (a') and low (b') stress. The effect of heterozygosity on fluctuating asymmetry may depend not only on the level of stress (a' versus b') but also on the effect that heterozygosity has on the shape or location of the curve describing the relationship between fluctuating asymmetry and stress [compare the relation between heterozygosity and fluctuating asymmetry at high stress (a') versus low stress (b') in figures a - c].

Table 1. Selected examples of subtle asymmetries as a percent of average character size (linear dimensions or counts). Note that the average differences between sides are very small.
A.R. Palmer Publications List, Asymmetry Page, Home Page
Original material on this page copyright © A. Richard Palmer. All rights reserved.
(revised Nov. 4, 2002)