This presentation will describe the physics (and math) of what occurs, for NON-physicist-types!
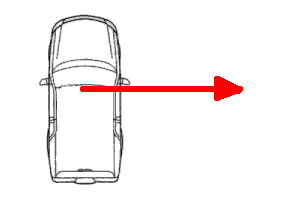First, whenever a vehicle turns, Newton's First Law indicates that it wants to
go straight, so the tires must therefore create a lateral "centripetal force".
This is entirely due to friction between the tires and the roadway. If the road
is icy and slick, there is generally not a high enough "static frictional
coefficient" to cause the force described here. The vehicle would then not roll
over but slide straight, possibly having DIFFERENT problems! A rollover
situation can only occur if there is enough friction between the tires and road
to create sufficient centripetal force.
We show the tire-road frictional force as the red arrow to the right in the drawing. That force, acting on the vehicle, is just the simple F = ma, expressed for a curved motion. For this example, we will consider a vehicle turning in a circular course, to the right, approximately like circling clockwise in an intersection, with a circle radius of 25 feet. Say the vehicle weighs 3200 pounds, and we will consider it moving at 20 mph. (20 mph is equal to about 29.3 feet/second). And the acceleration due to gravity is 32 feet/second/second. Now you know everything necessary!
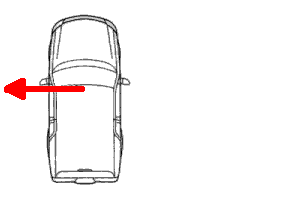With the force due to the tire-road friction being to the right, there is an
effect, often called centrifugal force, that then also exists to the left. It is
actually just the condition of the vehicle wanting to go straight (in accordance
with Newton's Laws) and so this centrifugal force (to the left) is exactly equal
in size with the centripetal force making the vehicle turn the corner. Sorry
about the confusing two words!
The F = ma for a circular motion is in the form F = (w * v * v)/(g * r). [w = vehicle weight; v = velocity/speed; r = circle radius; and g = acceleration due to gravity]. That version of Newton's Law is very straightforward. We do not need to get into its derivation here. This gives a centripetal force for our example: (F) = (3200 * 29.3 * 29.3)/(32 * 25) or around 3400 pounds!
That is the force that the tires traction must exert sideways on the vehicle to make it turn in the circle rather than going straight the way it would have normally wanted to go. (On an icy surface, nowhere near that much side force can be applied, and the vehicle slides straight instead of going around the turn. Now you know why!)
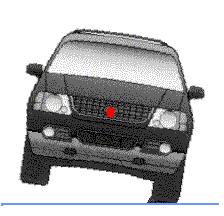
We have shown this force acting at one point of the vehicle, often called the center-of-gravity. Since the vehicle is one solid object, it can be mathematically treated as though all of its weight is at that one point. We are now going to change our position and look at the vehicle from the front, and we see the red spot that indicates the center-of-gravity.
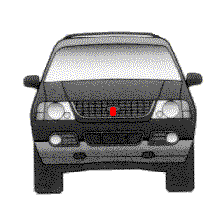OK.
That's the sideways force that has to be acting on the vehicle, in order for it
to go around that-sized circle at that speed. Now we need to look from the front
of the vehicle. We see the points where the tires contact the road. The distance
between them is called the "track". A red point is marked up on the body of the
vehicle, on its centerline. This is called the "center of gravity" of the
vehicle. It is the line through the length of the vehicle on which the entire
vehicle could be balanced. Imagine a giant barbecue spit rod going through the
vehicle at that point. As that rod would be turned, the vehicle would stay
balanced and would turn smoothly.
In other words, the entire weight of the vehicle acts as though it was at that point/line, height. Viewing from the front, we're looking at the end of that line, so it looks like a point in our drawing.
Here is the (3400 pound) centrifugal force that is acting on the vehicle, as
seen from the front, and still acting on the center-of-gravity.
In physics, a force can be thought of as a "resultant force" which is a combination of two "component forces."
We know that the tire treads are going to somehow be involved, especially since we know that on icy roads, the vehicle does not turn. So we know that the sideways force must be being applied between the tire treads and the roadway.
Our
(horizontal) centrifugal force can therefore be thought of as a combination of
two separate forces. One of the component forces is directly toward the tread of
the tire, as shown here. This component is actually the portion of the force
that actually acts to give the vehicle sideways force (through the tires'
friction with the road) to make it turn.
This is the physics way of showing how the tire treads are able to transfer a sideways force to the vehicle, to make it turn corners.
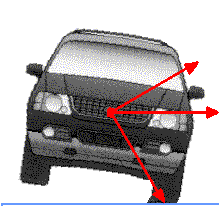
| In actual Physics, this subject is described in terms of something called "moments". A moment is a Force acting on an "arm" to cause a torque or a tendency to rotate. In this case, there is a moment that is due to the weight of the SUV, and that moment is a Vector aimed toward the FRONT of the vehicle (don't ask!) of W x r which has a magnitude W * r * cos(theta). The moment that is due to the centrifugal force is a Vector aimed toward the REAR of the vehicle of F * r which has a magnitude F * r * cos(90° - theta) or F * r * sin(theta). In the situation of being just about to roll over, these two must be equal, or F * sin(theta) = W * cos(theta), or F * sin(theta) / cos(theta) = W, or F * tan(theta) = W. Theta is the angle between the two red arrows shown above, and r is the distance between the center-of-gravity and the tire tread. |
The
other component force (of the centrifugal force) is at right angles to that
component, and so it is aimed upward and outward, as shown here. This component
would act to roll the vehicle over, around that tire tread.
We are concerned about the situation where the vehicle would ACTUALLY roll over sideways. From our front view, we then need to know the force necessary to act AT the center of gravity, AROUND one of the tire treads, as shown in this drawing. Let's call this Funknown. This force is upward at a (90 - theta) angle, which depends on the geometry of the vehicle. You can see that the magnitude of this component, Funknown, is Fcentrifugal * sin(theta).
You can see that this is the direction that a force would have to act in order to "roll" the vehicle over that tire's point of contact with the road.
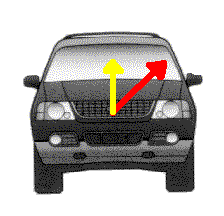We're not quite done! This angled force component can now be considered to be a
combination of a vertical and a horizontal force. If the vehicle is going to be
about to roll over, the UPWARD part of it (shown as a yellow arrow) is what we
are interested in and it must be at least exactly equal to the weight of the
vehicle. That would then LIFT the weight of the vehicle up off the roadway. The
(red) upward angled force gets a leverage advantage around the tire tread, and
so it is able to have a lifting effect greater than its own strength, actually,
equal to its strength divided by the cosine of theta. If the vehicle is about to
roll over, this lifting effect must be equal to the weight of the vehicle.
Funknown therefore equals Weight * cosine(theta), (or Weight =
Funknown / cos(theta). The cosine can never be more than 1.00, so
this means that its leveraged effect is always greater than its true force.
Standard geometry is then all that is needed to get actual numbers! It tells us that this angled (red) Funknown must therefore be the weight of the vehicle times the cosine of the angle shown (between the red and yellow arrow).
For a rollover to begin to occur,
That center of gravity is also above the ground. For a fairly tall vehicle like an SUV, it can commonly be 30" (or more) above the ground. Vehicle manufacturers used to divulge the height of the center-of-gravity of their vehicles, but they no longer do. For the vehicle illustrated, we believe that the center-of-gravity is probably around 34" above the road surface. Rather than using that value, we will again use a more generous (and more stable) 30" height for our example calculations.
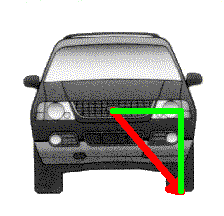Now, look again at the force acting between the tire tread and the
center-of-gravity of the vehicle (in red). This force is at an angle which has a
horizontal component (in green) proportional in length to half the track of the
vehicle. It also has a vertical component that is exactly proportional to the
height of the center-of-gravity above the roadway. We KNOW both of these
distances! Therefore, the angle at the CG (which we have been calling theta),
between the red and green lines, is the angle whose TANGENT is equal to (Height
of the CG)/(half the track) horizontally there. In the case of this example,
that vertical side is 30" and half-the-track is also 30". This means that the
angle we have been describing has a tangent of 30/30 or 1.000, and so the angle
is 45°.
Since we now know the angles in the triangles we have been dealing with, we can do the final calculations. Using the specific dimensions of ANY vehicle, it is therefore VERY easy to quickly calculate at what speed it would roll over! No "expert" could possibly get away with testifying in court that he does not know!
We have already determined that the actual lifting force on the center of gravity of the vehicle is the centrifugal force times the tangent of that angle, in other words, 3400 pounds times 1.000 or 3400 pounds vertical lifting effect!
Now, since the vehicle only weighs 3200 pounds, there is only 3200 pounds of gravitational force holding the vehicle down, and so this 3400 pound lifting force is enough to lift it up and roll it over.
That's all there is to the calculations! If the resultant vertical lifting force is less than the weight of the vehicle, it will not roll over; if it is more, it is certain to roll over.
In our example, at 20 mph, our vehicle would roll over when trying to turn in our 25-foot radius circle!
Actual SUVs are much heavier than we have used. However, the heavier weight increases the centrifugal force proportionally, which increases the force that acts to roll the vehicle, EXACTLY in the same proportion that the necessary lifting force is increased for the heavier vehicle. The actual overall weight of the vehicle does not alter these results! Only the track-width, the center-of-gravity height, the turning radius, and the vehicle speed are the ONLY variables!
Do you see that it is relatively simple to calculate these things? It would not be necessary to keep doing road tests with vehicles constantly going up on two wheels, as the government and testing labs keep seeming to do.
The general form of the calculations above is vertical LIFT = centrifugal force * Tangent(theta). In our case, that was 3400 * (1.000) or 3400 pounds lift. The PBS FrontLine program included some "manufacturer's experts" claiming that widening the track by two inches would do miracles. It is easy to do this math again to show that it would only make an incremental difference. In our example, widening the track by 2" makes our horizontal 30" into 31", while leaving the center of gravity height of 30" the same. It is easy to check that this geometrical change makes our 45 degree angle now become 44.06 degrees. The tangent of that angle is 0.9677. When put in our problem, we would now have 3400 * (0.9677) or 3290 pounds, STILL making the vehicle roll over! The dangerous lift is only minimally reduced, from 3400 to 3290 pounds! A two inch wider track would have extremely minimal benefit, as to safety from rollovers. Actually, where our original vehicle could have made our circle at up to 19.3 mph while being on the verge of rolling over, the one with the two inch wider track would be able to do it at 19.6 mph instead, less than half a mph improvement!
For comparison sake, a sporty car, also 3200 pounds, making the same circles
as described above, but with a center of gravity 14" above the ground, would
have the same centrifugal force, 3400 pounds.
But that angle theta would be
25 degrees, and the lift
calculation would be 3400 * (0.4667) or 1587 pounds.
Absolutely no danger of rollover, as 1587 pounds vertical lift is FAR less than
the 3200 pound vehicle weight. This explains why cars rarely roll over while the
taller SUVs do so far more often.
Once a rolling action has begun, everything gets a lot worse. This drawing shows
the situation once a vehicle has tilted only 10 degrees sideways. With some soft
vehicle suspensions, and under-inflated tires, this much of a tilt is nearly
possible while all the wheels are still on the pavement.
Let's look at how the forces we have been discussing change.
To start with, this doesn't look all that different.
But
compare this drawing with the similar ones above. You can see that the
center-of-gravity has gotten a little higher. At a 10° tilt, it is actually
raised up by 5.2". And if the tire's low pressure allows it to deform
horizontally, then it is less far horizontally from the tire footprint. We will
estimate 2". These two effects combine in making that important theta angle
bigger. We would now have (vertical) 30 + 5.2 or 35.2" and (horizontally) 30 - 2
or 28". The tangent is now 35.2/28, or 1.257. Our 3400 pound horizontal
centrifugal force then would have the effect of 3400 * 1.257 or 4274 pounds of
vertical lift!
The 3400 pound lifting/rolling effect has already gotten FAR greater, and there is no realistic chance of recovery. Where the problem began with a lifting force just a little more than the vehicle weight, as soon as the vehicle tilts, the geometry gets catastrophically worse.
FYI: This is why test vehicles always have those "training wheels" arms on them, because once a rollover begins, it gets so much worse so fast that even professional drivers have great difficulty in recovering.
(Once a rollover has begun, the geometry actually gets even more complicated, involving the dynamic rotational inertia of the vehicle and the fact that the effective weight of the vehicle becomes less (even zero as it crosses above the tire tread), but this last calculation essentially shows how the problem gets far worse as the rollover proceeds. These complicating effects all act to make the rollover effect even worse. All of the earlier "level vehicle" calculations were exactly correct.)
The other reason that the recommended low tire inflation pressures caused the accidents and deaths has to do with the normal way a tire functions. Each time a tire rotates, its sidewalls have to bend/deform as that part is in contact with the road, as it must briefly support the weight of the vehicle. This causes the sidewalls of the tire to flex every single revolution. This flexing ALWAYS creates frictional heat within the sidewalls of the tires. When the tire pressure is low, this flexing is greatly exaggerated, resulting in much more internal heating of the sidewalls of the tires. This is why a tire that is extremely low on air pressure quickly blows out, because the sidewalls flex so much that they overheat and then fail, permitting the internal pressure of the tire to suddenly burst out.
When tires have abnormally low air pressure in them, on long trips of high-speed highway driving, they are especially susceptible to the sidewalls overheating in this way. For this reason, it is quite understandable that many tires failed and caused terrible accidents on those Ford vehicles and on all other SUV vehicles that recommend low tire pressures. This is actually an effect whether the vehicle is traveling straight or turning. If a particular tire had even a hint of a problem on its own, that situation would ensure that it would fail. So, whether or not the Firestone tires had any drastic flaw, even if they have a tiny additional inclination of a flaw as compared to other brands, the effect would have been tremendously magnified by the circumstances of the low recommended tire air pressures in those vehicles. The natural instability of the high center-of-gravity vehicles added to the problem, to cause the many rollovers once the vehicle got turned a little sideways.
The driving public seems to think that these problems have "gone away". They have not. All of the millions of NEW SUVs being manufactured and sold, still have this tremendous tendency toward rollover accidents. Just widening the track a few inches will not make them materially safer, as shown above. The very nature of a tall vehicle which is intended for use at high speed and in potentially abrupt maneuvers, ensures continuing danger. It seems amazing to me that so many millions of mothers entrust their children to regularly riding in such vehicles! They clearly have very little idea of how dangerous they actually are. It would seem that the manufacturers must be doing an effective effort at minimizing publicity of the many accidents! It's hard to imagine how they will be able to financially survive once tens of thousands of settlements for millions of dollars each will start being necessary.
Interestingly, the manufacturers cannot claim to not be aware of these matters! For example, Ford's SUV vehicles have wider track dimensions VERY much in line with these calculations! For example, their very tall Excursion (77.2" tall) has a MUCH wider track (64" compared to 56") as compared to their own Explorer Sport SUV, which is 68.4" tall. It is obvious from that that they are VERY aware of needing a wider track dimension for the even more unstable taller models. That means that they have always known what they were doing to begin with! And, assuming that their engineers were capable of the High School Physics presented here, they have been aware of the instabilities that are direct consequences of their decisions.
Given how simple these calculations are, it is really disappointing that no one seems to be in a position to challenge the "engineering" of the carmakers! To watch in that PBS program, an "expert" representing a carmaker testifying that he just didn't know how great the benefit would be of widening the track two inches, was appalling! Tell them to get any high school Physics student to explain it to them! The calculations above show how simple those calculations are! There ARE no "complicated" calculations to do! This is all of it!
( http://mb-soft.com/public/othersci.html )
C Johnson, BA Physics, Univ of Chicago